確率はこれで完璧!ハッとめざめる確率の4ポイント

関数、図形など、数学には様々な単元が存在する。
その中でも、特に苦手な人はとことん苦手なのが確率である。
センター試験を例にすると、10分程度で満点が取れる人もいれば最初の二、三問以降全く完答できない人がいる。
もちろん他分野であっても10分で完答できる人も全然できない人もいるが、確率という分野では特にそれが顕著である。
今回はそんな確率を苦手としている人、もっと得意にしたい人のための参考書、ハッとめざめる確率(通称ハッ確)について解説する。

この一冊をこの記事通りに使えば、苦手だった確率が克服できるだけでなく、なんと得意になってしまうのだ。
是非この記事を参考にしてハッ確で確率を得意にしよう！

『確率』の難しさ

はじめに、確率はなぜ得意不得意がハッキリ分かれるのか、確率という分野のなにが難しいのかについて記述する。
確率が厄介なのは主に三つの理由がある。
まずは確率という分野が厄介な三つの理由をしっかり読んで理解を深めよう。

他分野から独立している

まずは、数学の分野ごとの関連性についてまとめたこの表を見てほしい。

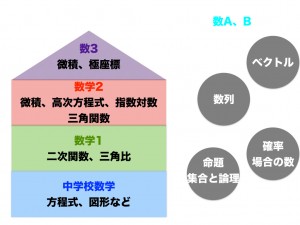
確率は数学Aの分野であり、数学Aは大きく分けて命題、確率、図形の三つに分かれる。
しかし同じ数Aといっても、この三つの分野に全く関連性は無く、数Aに続く科目である数学Bにおいても、これら三分野との関連性が強い分野はほぼ無いのである。
（しいて言えば数Bの数列に出てくる確率漸化式くらいだ。）
逆に数一、数二を見てみると分野ごとの関連性が非常に高いことが分かる。
高次方程式、指数対数などは二次方程式の応用であるし、三角関数は三角比の応用である。
そして、数二では数一で学んだことを活用する機会が非常に多い。
つまり、暫く数一に触れてなかったり、数一を真面目に勉強してこなかったとしても数二をやるうちに自然と数一の力がつくということだ。
実際筆者も高校一年生の頃、勉強の手を抜いて高一の頃の数一の成績は酷いものであった。
しかし高校二年生で数二を奮起したところ、気づいたら数一の成績はかなり上がっていた。数二の実力を付けることは、そのまま数一の実力を付けることになるのだ。
しかし、そう上手くいかないのがこの確率である。
同じように数Bから奮起した筆者だったが、受験生になってからの数Aの成績は高校一年生のころと全く変わらず、酷いものだった。
これが確率が厄介な理由の一つめだ。
受験において、配点や出題頻度が高いのにも関わらず、受験への意識が低い高校一年生(主に)の間に学習を終えてしまい、その後ほとんど触れられない。
そのため、筆者のように高校二年生や受験生になってから奮起した人や、定期の一夜漬けのみしかしてこなかった人にとっては、確率が高い確率で非常に大きな障害になるのだ。

公式の汎用性が低い

二つ目の理由としては公式の汎用性が低いことである。
本来あまり良いことではないが、センター試験序盤などの受験数学の簡単な問題は頭を使わなくてもいつものパターンで解けてしまうことがかなり多い。
たとえば二次関数では、とりあえず平方完成して頂点と最大値,最小値を求めれば、基本問題はほとんど解けてしまうし、三角関数などであれば、とりあえず公式に入れてしまえば解けることが多い。
このように、受験数学の他分野においては公式の汎用性というものがかなり高くなっている。
まずは公式を利用できるようになることが理解に向けての第一歩へと繋がるのだ。
しかし確率においてはそれが全くの反対となるのだ。
確率にもP（パーミテーション）やC（コンビネーション）といった公式は存在する。
しかし、本書(ハッとめざめる確率)において作者はこのように記述している。

CやPの使い方を教える問題や超基本の問題は別にして
いきなりCやPを使おうとしてはいけない
【『ハッと目覚める確率』　はじめに　より】

これは確率という分野においては非常に的を射ているのである。
簡単な問題、典型問題においても考えるウェイトが高い確率という分野においては、できる人ほど公式を使わないのである。
数学の先生の中にはPを使わずCのみしか使わない先生も多くいる。実際に筆者に確率を教えてくれた先生がそうであったし、筆者も受験においてPを使ったことはなかった。
確率ができない人にとってこの話は目からウロコだったのではないだろうか。
公式の汎用性が他分野に比べて極端に低いということが理由の二つ目だ。

「見落とし」を作らない『コツ』がある

最後の理由としては確率には『コツ』が存在することであろう。
確率の問題の解き方は

といった流れを辿る。
そして、確率の問題を確実に正答するためには「見落とし」が無いことが必要不可欠となってくる。
しかし「見落とし」のないルールを設定するためにはいくつかの『コツ』が必要になってくるのだ。
そして、この『コツ』はどこかに書いてあるものではなく、また常に同じものとも限らない。
つまり、自分で演習を繰り返していくうちに自然と身につけるしかないのだ。
演習を積んできちんと復習をすれば自然と身につくものであるが、確率から逃げ続けていればまず出来るようにはならないだろう。
以上3点が確率が苦手な人が多い理由であった。

２番目と３番目から分かることだが、つまるところ確率は中級レベルの問題であってもしっかりと頭を使わなければならないのである。
確率では公式の暗記やパターンの暗記では思うように点数が取れないのが特徴だ。
このことを理解したうえで、ハッとめざめる確率、通称ハッ確の説明に移っていこう。

ハッとめざめる確率

ハッとめざめる確率は平成13年に初版が発売された確率、場合の数を専門とした参考書である。
著者は東京大学理科I類出身の予備校講師、安田亨氏だ。
著書の中で氏は自らも場合の数は苦手だったと書いており、そのため場合の数と確率が本当に苦手な高校生にとっても非常に理解しやすい参考書になっている。

私が受けた数学のテストで最低点は34点、高校一年生のときの場合の数のものです。
怠けたからではありません。有名な参考書を三回まわりやってもよくわからなかったのです。
ハッとめざめる確率　本書の利用法　より

基本的に文章は話し言葉で構成されておりイラストも多く使われているため、親しみやすいものとなっている。

ハッ確をつかうことによるメリット

まずはハッ確を使用するメリットについて説明しようと思う。
メリットは本書にあるように、基礎から解説を始め、難関校も含めた合否を分ける問題を解けるようになることである。

知識のない人にも分かるように書いていきます。
初めのうちは、ある程度学んだ人は「そんなこと知っているよ」という部分も多いでしょう。
説明が基礎的で、しかも繰り返しになるために、しつこいと感じることがあるかもしれません。
【『ハッとめざめる確率』　基本の約束　より】

そのため、本当に何も分からない人であっても安心して勉強を始めることができる。
また、

基礎から解説しますが、最終的な目標は難関校も含めた合否を分ける問題を解けるようにすることです。

とあるように、中、後半からは非常に難易度の高い問題が並ぶ。
丁寧な解説がついた良問ばかりであるが、確率が得意な人であっても持て余す問題が多いだろう。
そのため、さらに確率を極め、得点源としたい学生に対しても勧めることができる。

ハッ確をつかうことによる注意点

初級者から上級者まで使えるということは、ウラを返せば非常に量が多いということだ。
確かに確率は出題頻度も高く、重要な単元であるが、1A2B選択者からすれば16、理系からすれば20単元のうちの一つに過ぎない。
そんな単元一つに全287ページを費やすのは手間をかけ過ぎである。
全ページをやりきってもいい人は、高校一年生から東京一工レベルを志す人か、他教科、他分野は全て完璧だが確率だけ全くできない人くらいのものだ。
いくら確率が苦手だからといって、ハッ確を1から10までやろうとしては確実にパンクしてしまう。
ハッ確を使用するうえで大切なのは、自分の実力、目標、他教科との兼ね合いを考えて使用するページを決めることである。

　ハッ確の効率的な使用法4ポイント

最後に、ハッ確の効率的な使用法について述べようと思う。
この参考書の使い方について作者は

勉強のしかたは人によっていろいろです。自分の方法が確立している人は自由に読んでください、どんどん解答を読むもよし、まずは鉛筆を持って解くもよし

と述べており、実際その通りである。
しかしそのように言っておきながら、その後に述べている安田氏の勉強法があまりにも完璧なので簡単にまとめさせていただいた。

ポイント1　公式の理解、暗記

まずは例題の前に基本公式の解説をしている部分があるので、これを熟読し、理解しよう。
理解できているかどうかの基準は自分で証明が出来るかどうかである。必ずこのレベルまで理解をもって行こう。
PとCの区別など、公式が紛らわしい場合の数と確率において、証明のできない公式を使うことは非常に危険だ。

ポイント2　演習、復習

まずは例題を読んで、自分で問題を解いてみよう。
15分程度考え、解けなかったり、上手な解法で解けなかった場合や日本語がうまく書けないなら、解答を熟読してほしい。
解答を一切見ないで解答を再現できるようになろう。
これは解答の丸暗記をするという意味でなく、考え方や解答に至るまでの流れを暗記するという意味である。

ポイント3　いさぎよく飛ばす

解答をよんでもどうしても理解できない、よくわからない。
そういった問題や考え方が出てきた時は、焦らず一回で理解しようとせず、印をつけてとばして先に行ってしまおう。

理解しがたい点、ピンとこない点が出てきたら印をつけとばして先にいく。頭の貯蔵庫に入れておく。
発酵、熟成が進むと分かるときがきます。
【『ハッとめざめる確率』　読み方と勉強法について　より】

ポイント4 普通の解法と「うまい」解法

解説は、普通の解法とうまい解法を述べている部分があります。
正攻法の習得と発想の幅を広げることが学習の目的ですから、どちらの考えも学んでください。

確率に限らず、多くの数学の問題には発想の転換による「うまい」解き方というものが存在する。
正攻法だけでなく、こういった賢い方法も学ぶことによって発想の幅は広がっていくのである。
これは数学全体において非常に重要な考え方だ。

まとめ

今回はハッとめざめる数学の解説と確率という分野に対しての記事であった。
今回の記事を読んだ確率を苦手としている高校生は、自分がなぜ確率が苦手なのか、理解してもらえたと思う。
ハッとめざめる確率は、慶早進学塾でも採用している良書である。
気になった方はぜひ書店に行って手に取ってみてほしい。必ずあなたの成績の上昇を促してくれるはずだ。